Non-Linear Curve Fit

DataView implements a general non-linear curve fitting routine adapted from that of Prof. John C. Pezzullo, whose generous help I gratefully acknowledge. The concept is that a collection of X-Y data values is presumed to follow a mathematical function (the model), such as exponential decay. Curve fitting is the process of finding the parameters of the function that enable it to best fit to the data.

In summary, the algorithm attempts to find the set of parameters that minimize the sum of squared residuals (SSR, also known as the residual sum of squares, RSS), where a residual is the difference between the actual value of a point and its value as predicted by the model with a given set of parameters. It assumes that the deviations from the model are a result of Gaussian noise. This may not be strictly true for neural data (membrane noise resulting from background synaptic activity may show strong serial correlation), but nonetheless the algorithm is often successful at finding a set of parameters that provide a good fit to the data. Please consult Prof. Pezzullo's linked web page for full details of the algorithm.

The X-Y data can either be a time-slice section within a standard data trace, in which case the X values are the relative time within the section and increase throughout the collection with an equal step size set by the sample interval, or an independent collection of X-Y values derived from an external source, in which case X values need not be evenly spaced, and may not necessarily be in order.

Trace Data Analysis

• Load the file noisy sine.
  This file was constructed in DataView, and the trace label shows the formula that was used.
• Select the Analyse: Non-linear curve fit menu command to activate the Curve fit  dialog.

The main window in this dialog box shows the section of the data trace that you will analyse. This is either the entire region of the main display, or, if you had placed two vertical cursors in the display, the region bracketed by those cursors. The red line plots the expression shown in the Equation edit box, and will eventually show the fitted curve.

Non-linear curve fitting requires three user inputs.

First you have to define the “model”, i.e. the equation for the function that you are trying to fit. The data clearly suggest an offset sine wave (and of course we know that this is the case from the formula shown in the trace label), but to make life more interesting, let’s fit to a cosine curve.

• Type (or copy-and-paste) the expression cos(a + b * t) + c into the Equation edit box at the top of the dialog.

In this expression t is time, as in the expression used to plot the function in the first place. The a parameter defines the phase shift for the cosine curve. The b parameter (in combination with the time t) defines the frequency of the cosine wave, while the c parameter defines the vertical offset. These are the three parameters to which we wish to fit values.

• If possible, you should enter an estimate of the signal noise (as standard deviation) into the Data SD edit box. We do in fact know that the noise SD is 0.1 (since that was how the data were constructed) so enter this value. If you do not know what the signal SD is, just leave it at its default value of 1. The noise estimate does not affect the curve fitting, but it does affect the goodness-of-fit metric (see below).

Now you have to enter estimates of the initial values for the parameters. Curve-fitting progresses more quickly, and is more likely to result in a realistic result, if your initial estimates are reasonable.

DataView allows you to experiment with initial values and to see the results in the red line on the display.

• Enter 0 into each of the first 3 parameter edit boxes, and observe the red line is flat at a level equivalent to the value 1 (cos(0) is indeed 1).
• The data are obviously time-dependent, so enter 1 into the b (frequency) parameter box. The red line now at least shows time variance, although it is obviously at much too high a frequency and too low on the screen.
• Enter 0.1 into b. The frequency is still too high.
• Enter 0.01 into b. The frequency is now too low, but it’s time to give it a try.
• Click the Curve fit button.

With these settings, with luck and a following wind, the red line will adjust to fit pretty much exactly to the data. If it heads “in the right direction” but is still not a good fit, click Curve fit again. If there is still no fit, try adjusting the values by hand to get a better initial fit.

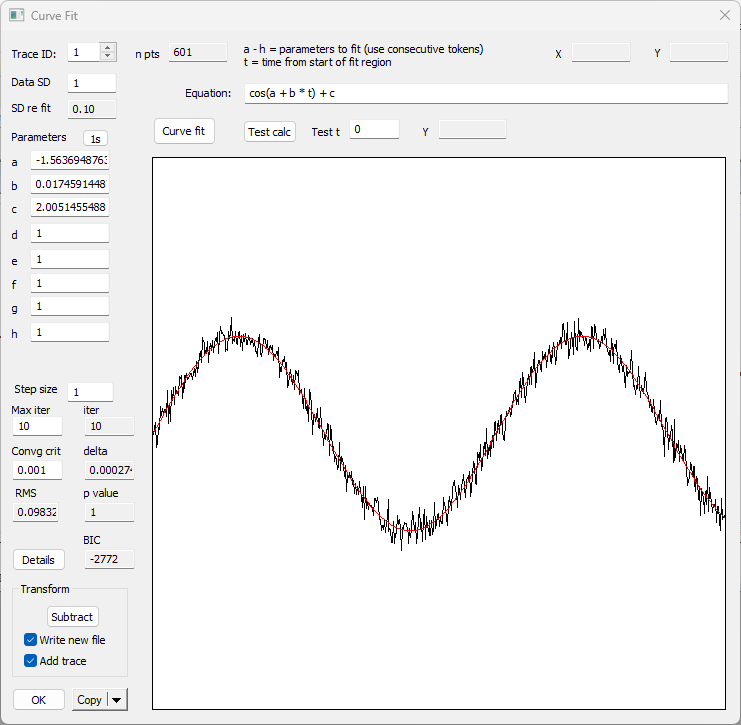
The parameters in the edit boxes have adjusted to reflect fitted values. The offset parameter c is extremely close to the formula value of 2. The phase parameter a is very nearly equal to -π/2 (-1.5708), which, converted from radians to degrees gives -90°, which is the correct phase shift to convert from cosine to sine. The frequency parameter b is very nearly equal to 2π/360 (0.017454), which is what we used to generate the curve in the first place.

At the bottom of the dialog box is a display showing the RMS, which is a goodness-of-fit measure. It is normalised so that if the S.D. parameter is accurate, then an RMS value close to 1 indicates a good fit between the data and the model (i.e. deviations from the model prediction are in line with those that would be expected from the noise in the data), while values much greater than 1 indicate a poor fit. The p value indicates the probability that deviations from the fitted curve which are found in the data could have arisen by chance (so low p values indicate that the data are not a good fit to the model).

The accuracy of the RMS and p values are highly dependent on the accuracy of the noise estimate entered as the Data S.D. above. If you just enter 1, then the RMS is simply the square root of the mean of the SSR (sum of squared residuals), which is the population standard deviation. If you are sure that your choice of model is correct then you could use this as the S.D. value and re-fit to find a new p value for the goodness-of-fit value. But of course if you do this you could not use a good fit as quantitative evidence that the model is correct – that would be a circular argument.

• If you want to see full details of the analysis, click the Details button. This shows various parameters associated with the fitting process, including a full list of the raw data values and their equivalent fitted values, and the estimated error range of each point. You may need to refer to a statistics text book to interpret further details of this output.

The curve fit process works by iteratively adjusting the parameters so as to minimize the difference between the data and the red line. The iterations stop either when the number of iterations exceeds that set in the Max iter edit box, or when the Convergence criterion is met. This latter is defined as the greatest percentage change that occurs in any parameter between iterations. Thus when parameters are changing by only very small amounts between iterations, it is unlikely that further iterations will significantly improve the fit.

Sometimes the curve fitting process just does not work; the red line may hover around some function shape that is obviously wrong, or may “blow up” and yield ridiculous shapes. This is particularly likely if your initial parameter estimates are wildly wrong.

• Reset all the parameters to 0 by clicking the 0s button.
• Click Curve fit, and observe that the red line (probably) goes off generating shapes which are obviously not fitting the actual data.

Improving fits

If the fit obviously fails, the first thing to do is to check whether the model itself may be totally wrong. If you are happy with the model, try to improve the initial estimates of parameters that you enter. Get the red line fitting as closely as possible to the data before you click the Curve fit button. If the fit still fails, try reducing the Step size parameter. This will reduce the speed of fitting, but may well head off errors before they become critical. If the fit looks like it is working but is still not very good after 10 iterations, then just click Curve fit again. Alternatively, increase the Max iter parameter to a larger number. A useful strategy is to start curve fitting with a small Step size (e.g. 0.1) but only allow 10 iterations. If the fit looks like it is heading in the right direction, then increase the number of iterations to a large number (e.g. 100), and wait for convergence.

Choosing Between Models with BIC

In most real-world situations we do not know for sure what underlying process produces a particular waveform.

• Click OK to dismiss the Curve fit dialog box
• Place two vertical cursors on the screen at 260 and 520 ms respectively (use the Cursors: Place at time menu command).
• Now re-start Analyse: Non-linear curve fit.

We now have only a fragment of the sine wave visible, and without prior knowledge we might be tempted to try fitting a 3rd-order polynomial to the data.

• Enter a * t ^ 3 + b * t ^ 2 + c * t + d into the equation editor. Note that a to d are the coefficients of the polynomial, which are the parameters we want to fit.
• Enter 0 into the a, b and d parameter boxes, and 0.01 into the c box. This gives us a linear equation (1st-order polynomial) with a slope approximately in line with the rising phase of the curve. It is a good enough starting position.
• Click Curve fit.

We get a reasonable fit to the curve, with the RMS value close to 1, and the p value that is insignificant. However, note that the fit does not meet the convergence criterion.

• Increase the Iterations to 100, and reduce the Step size to 0.1.
• Click Curve fit again to see if we can improve the fit.
  Even with repeated fitting, the convergence criterion cannot be met.
• Note (and probably write down), the BIC value. In my run this was -1139, although the exact value may vary depending on how many fits you attempted. Now we will go back to fitting a cosine wave.
• Copy the cosine equation (cos(a + b * t) + c) into the equation editor as above, and re-enter a = 0, b = 0.01 and c = 0 as the initial values of parameters.
• Click Curve fit again. Note that after possibly a couple of clicks, convergence is achieved.
• Note that the RMS and p values are good, and that the BIC value is now -1177; it is thus a lower value than that achieved by the polynomial fit.

In general, if choosing between alternative models which are apparently equally plausible, one should choose the model which generates the lowest (most negative) BIC value for the same set of data. In this case we know that the data were generated from a sine wave, and so the relative BIC value has led us to the correct decision.

BIC – the Bayesian Information Criterion

You may have already come across the BIC in terms of fitting histogram models by maximum likelihood, but now we consider it in the context of least squares fitting. If we have various alternative models that could fit a set of data, how do we decide which one provides the “best” description of the data? A standard metric for measuring goodness-of-fit is the sum of squared residuals (SSR) as described above. The lower the SSR, the better the fit. Indeed, the curve fitting algorithm used in DataView works by finding the set of parameters that minimize the SSR.

At first sight this would seem to solve the problem – just select the model with the lowest SSR. However, this does not take into account the complexity of the model. If we make the model complex enough, then we can make it produce an exact fit to any data. However, Occam’s Razor suggests that we should prefer a simple model with just a few parameters that produces a reasonable fit, over one with a thousand parameters, even if the latter produces a somewhat better fit. The Bayesian Information Criterion (BIC) formalizes this intuition, and provides a mathematical basis for deciding on the trade-off between complexity and goodness-of-fit. It is based on information theory, and I certainly don’t understand the full the theoretical basis, but its formulation is quite simple.

         BIC = n log(SSR/n) + k log(n)
where n is the number of data points, and k is the number of parameters. SSR/n is the same as the variance of the noise.
We can see that having a poorer fit and hence a larger SSR produces a larger BIC, and that having more parameters produces a large BIC. The formulation above determines the trade-off between these two influences. If we choose the model with the lower BIC, we will have chosen the better model.

BIC and Curve-Fit Caveats

• An important caveat is that the BIC is only relative. One can compare the BICs of two models and choose the one with the lower BIC, but the actual BIC value tells us nothing about how “good” the chosen model actually is.
• The BIC should be calculated using exactly the same raw data in the various models being compared. The data should be in the same domain (i.e. if comparing the BICs of two models one should not use raw data in one model and log-transformed data in the other).
• The noise in the data should be “IID Gaussian” – independent and identically distributed, following a Gaussian distribution. This is the constraint that is most likely to be violated with real data. Membrane noise often shows serial correlation (particularly if it is generated by background synaptic activity or mains interference) so it is not independent, and it may not be Gaussian in distribution. However, even though this constraint is often not fully met, in practice the curve-fitting algorithm seems to perform well with real data. The main consequence of any violation is that one should not place absolute trust in the precise p-values and BIC values, but take them as guidelines rather than rules.

Remove the Trendline

Sometimes it is the residuals (i.e. the deviations from the fitted curve) that contain the information of interest. This would be the case if a recording was contaminated by some regular shift in baseline, such as an exponential drop over the course of a recording (but see Remove exponential drop for a specialist routine for calcium imaging experiments). The Curve Fit dialog allows you to construct a trace showing just the residuals.

Assuming that you have already fitted a curve to the noisy sine data as described above:

• Click the Subtract button in the Transform frame at the bottom-left of the dialog.
• Enter a new filename when prompted.

When the file loads, the second trace shows just the deviations of the data in trace one from the fitted curve. In this case the deviations are just random noise, but in a real experiment they might well be informative.

External Data Analysis

As well as fitting a curve to a data trace (or section of a trace: see Trace Analysis above) DataView can also fit a curve to data imported from another program, or from an analysis routine within DataView itself. A full description of the process and its controlling options is given above following the Trace Analysis section, but here are some key differences:

1. Data must be pasted from the clipboard or loaded from a file, they are not automatically read from a trace. In either case the format is simple: the data should be in two tab- or comma-separated columns, with the left column containing the X values and the right column containing the Y values. There can be a text header row, but this is ignored.
2. The X values of the data do not have to be evenly spaced.
3. The data do not have to be in X-order, although the graphical display can be simpler to interpret if they are.

• Select the data below, and copy them to the clipboard. These are the example data used by Prof. Pezzullo, and show the rate of cooling of a cup of coffee. However, the data have been slightly shuffled, so that the time values are not in sequence. This is just for illustration.

		Time (min),		Temp (°F)
		5, 			155
		0, 			210 
		1, 			198
		2, 			187
		10, 			121
		30, 			77
		45, 			71
		15, 			103
		60, 			70            

• Activate the Analyse: Curve fit: external data menu command to open the Non-LInear Curve Fit dialog. Unlike most analysis routines, this is available even if no data file is loaded.
• Click the Paste button within the dialog.

You can now see the X-Y values from the external source in black, plus a red line showing the fit to the data using the default equation and parameters (these are just holding values and have no relevance to the current tutorial).

Because the rows are not sorted in X value order, the lines connecting the data points are jagged. While this does not matter for curve fitting, it makes it more difficult to see the trend in the data.

• Click the Sort button.

The rows are now sorted in ascending X (time) order.

Cooling approximately follows a declining exponential time course (Newton's law of cooling) which can be expressed thus:

(a - b) * exp(x / -c) + b

where a is the initial temperature, b is the environmental temperature towards which the object cools, and c is a time constant.

• Copy-and-paste the equation into the equation edit box within the dialog.

Examination of the raw data shows that the starting temperature is about 200 (the temperature is in degrees Fahrenheit, so this is near boiling), the ending temperature is about 60 (a coolish room), and the time constant looks to be about 15 minutes (that's a quarter across the graph).

• Enter 200, 60 and 15 into a, b and c respectively

The red fit line now lines up quite closely with the black raw data line.

• Click the Curve fit button above the graph.

The red fit line rapidly adjusts to a very close fit to the black data line. The numerical values of the parameters can be read from the a, b and c parameter boxes.

Details about the other controls and parameters were given earlier, so you can go back and read them if you have not already done so.

Continuous curve plot

By default, DataView just plots a "join the dots" display where each fitted XY pair is connected by a straight line. However, it may be better display the equation output as a continuous curve.

• Check the Continous fit curve box to plot the curve.

 

 

---